We adore math art projects. I’ve been eyeing the idea of using parabolic curves in a creative endeavor with my math-loving kid for a while. I was experimenting in my own art journal with the groovy way you can fool the eye into thinking a group of straight lines is actually a curve when my 10 year old leaned over and said, “That is so cool!!”
That’s when I knew I had a great math art activity for us to do together. Since my sons are naturally drawn to S.T.E.M. – themed activities, I do try and find ways to sneak in the “A” to make it S.T.E.A.M., in which the “A” stands for Art and Design. Last week I shared our Fibonacci Art Project, and like that lesson, our exploration of parabolic curves is just that: a process-based exploration.
I’ll give you the basic instructions for how to make parabolic curves and then let you and your kids explore math art on your own! (Note: this post contains affiliate links)
What you need:
- Pencil (believe me, you do not want to start with ink!)
- Eraser (see above!)
- Pens. We’ve switched from Sharpies to Flair pens. You only have to smell them to find out why.
- Rulers or straight edges. It’s easier to create squares if you have a triangle or t-square. I think it’s well worth having a math set. They aren’t very expensive and they are loads of fun, not to mention being handy for school projects.
- Protractor. Optional, but a must if you want to do a circle design. We get a lot of use from our 360 degrees protractor
- Paper. We made ours in our art journal. The mixed media visual art journal is our absolute favorite, which regular readers (waving hello!) know that I frequently sing the praises of. Alternatively, you can use graph paper.
- Sharpener. You want sharp, sharp pencils for this project!
- Colored pencils. Optional, but fun.
Instructions:
1. Create a set of crossed lines, preferably at a 90 degree angle. (Kids can experiment with different angles once they’ve learned the basics.) For ease, make sure each line is an even measurement. We used 1 cm and 5mm increments
2. Divide the lines into equal divisions. In my example I’ve uses 5 millimeter increments.
3. Draw angled lines. Start on the bottom line in the left hand corner at the furthest mark. (See photo above.) Draw a line from the mark to the first mark on the adjacent line. Draw a second line from the second furthest mark and connect it to the second mark on the adjacent line. (See photo below.)
4. Continue until all the lines have been drawn.
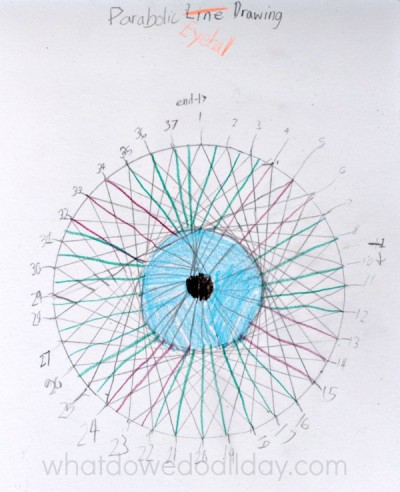
TIP: The starting/ending points of the first and last few lines can get “lost”. To make it easier, number the marks. (See photo below)
Voila! A “curved” line appears.
5. Optional: go over pencil lines with marker and/or use colored pencils to create colorful designs.
TIP: For kids just starting out, divide the lines with wider marks. My example above is 5 mm, but Kiddo preferred to work with 1 cm sections.
Variations:
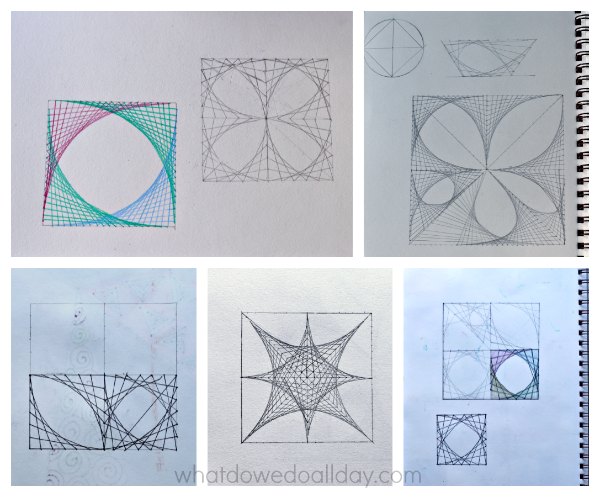
1. A single parabolic curve, while cool, is just the beginning. Encourage your kids to create boxes, triangles, and interlocking shapes as a basis to create elaborate math art designs!
2. Connect the dots in a circle! My son created a “parabolic eyeball”.
For inspiration, here are some of our experiments, straight from our art journals. (You can see I need to work on my photo editing skills, ha ha ha.)
Watch more of our math art ideas in action:
MORE: Tessellations and the Pi Skyline are two of our favorite math drawing projects. Little kids can practice connecting the dots, too, with a giant dot to dot. Or check out more fantastic patterns in these math art books.
Lise says
January 20, 2015 at 8:29 pmThis is so cool!
I was just creating designs with pattern blocks the other day with my daughter, and we got all excited about how it began to resemble a circle, even though it was all straight lines and angles. This is a great way to take that a step further…
Erica MomandKiddo says
January 21, 2015 at 8:59 amI hope you enjoy it!
Science Kiddo says
January 24, 2015 at 3:01 amI love this math art! I used to make these kinds of pictures when I was a kid, just for fun. Thanks for linking up at STEM Saturday!
Susan says
May 14, 2015 at 10:47 pmI remember making patterns like this when I was in elementary school. Drawing the lines was only one way to do it – we also used thin card or counted cross-stitch fabric and a needle and embroidery thread, or we used pieces of wood with nails banged in to them. I remember visiting a classmate’s home and her mother had one that she’d made hanging on the wall as artwork – painted black wood, black nails, and white threads. Precision placing of the holes or nails was key to a good design!
Erica MomandKiddo says
May 16, 2015 at 3:56 pmString art is very cool.
Rachel Price says
May 18, 2015 at 6:00 pmHi,
This looks very effective, thanks for sharing. I’m wondering what ‘math’ you taught alongside this. what about parabolas did you discuss? This is pushing my own knowledge so I’d love to make some stronger math links as well as making a nice design.
Thanks
Erica MomandKiddo says
May 20, 2015 at 6:05 amI don’t homeschool so this was primarily for fun. I like to show my son how math can produce wonderful art. But of course you can certainly discuss the characteristics of parabola, their relationship to conical structures, and also symmetry.